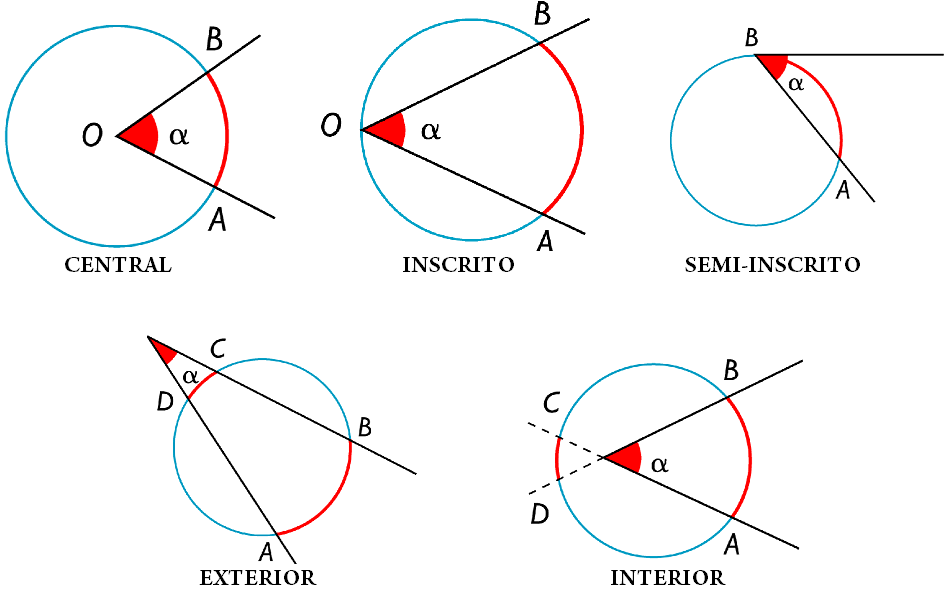
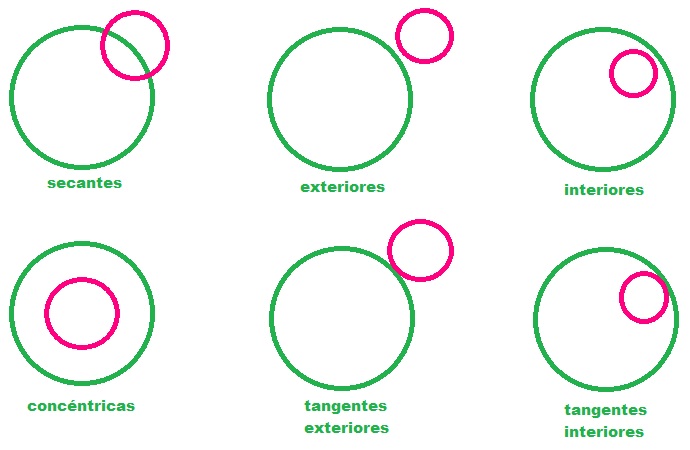
Un círculo, en geometría euclídea, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida.
Existen diferentes tipos de circulos, y entre ellos están: Elipse, Ovoide, Óvalo, etc.
Hoy les hablaré sobre los Óvalos. Un óvalo, en geometría, es un círculo plano que se asemeja a una forma ovoide o elíptica. A diferencia de otras curvas, el término óvalo no está claramente definido, y muchas curvas diferentes son llamadas óvalos. Éstas tienen en común lo siguiente:
-Su forma no se aparta mucho de la de una circunferencia o una elipse,
-Suelen tener uno o dos ejes de simetría y
-Son curvas planas diferenciables (textura suave), simples (no se auto-intersecan), convexas, y cerradas.
Aquí les dejo un mapa mental sobre el óvalo.
Un óvalo puede ser construido de diferentes maneras, entre ellas están:
-Construir un óvalo conociendo su eje mayor:
-Construir un óvalo conociendo su eje menor:
-Construir un óvalo conociendo sus dos ejes:
Espero que esto les haya servido. ¡Hasta luego!